Distribución Binomial
Cuando el experimento a realizar posee las siguientes características:- Existe una serie de N ensayos,
- En cada ensayo hay sólo dos posibles resultados. Los resultados de cada prueba de un experimento se clasifican en una de dos categorías exclusivas (mutuamente excluyentes), un éxito o un fracaso.
- La probabilidad de éxito y fracaso permanece igual en todas las pruebas o ensayos.
- Las pruebas son independientes, lo que significa que el resultado de una prueba o ensayo no afecta el resultado en cualquier otra.
Para denotar que los valores de probabilidad serán hallados a través de una binomial, denotaremos P(X) = b(x; n, π). Los valores de probabilidad para cada valor de la variable aleatoria se pueden calcular a través de la siguiente fórmula:
Donde:
- C: Combinación.
- n: Número de pruebas
- x: Es la variable aleatoria, definida como el número de éxitos.
- π: Número de Éxitos.
Si quisiéramos calcular la media y la varianza de una distribución binomial, se haría a través de:
Ejemplo 19. Existen 5 vuelos comerciales en una línea aérea. La probabilidad de que un vuelo llegue tarde es de 20%. ¿Cuál es la probabilidad de que ningún vuelo llegue tarde hoy? ¿Cuál es la probabilidad de que un vuelo llegue tarde hoy?
Se define:
- X: N° de vuelos que llegan tarde, de un total de 5 vuelos.
- n = 5; Probabilidad de éxito = 20%
- P(x) = b(x; 5, 20%)
En el primer caso tendríamos:
La probabilidad de que ningún vuelo llegue tarde es de 32,77%
En el segundo caso tenemos: n = 5; x = 1; probabilidad de éxito = 20%
Así mismo, la media y varianza de esta distribución de probabilidad es de:
Como parte del ejercicio, usted calcule la distribución de probabilidad (todos los valores posibles de la variable aleatoria con sus respectivas probabilidades) y verifique los valores de la media y la varianza.
Ejemplo 20. Del total de engranajes producidos por una fresadora de alta velocidad, 5% están defectuosos. Se seleccionan 6 engranajes al azar y se observa si están defectuosos. Construya la distribución de probabilidad para este experimento.
Aquí se observa que se cumplen las condiciones de la distribución binomial. a) Existen solo dos posibles resultados, b) existe un número de pruebas fijo, c) existe una probabilidad constante de éxito, d) las pruebas son independientes.
Se define la variable aleatoria como:
- X: número de engranajes defectuosos presentes, en una selección de 6 engranajes.
- n = 6; Probabilidad de éxito = 5%
- P(x) = b(x; 6, 5%)
Aplicando la fórmula de la distribución binomial obtenemos:
Adicionalmente podemos determinar su media y su varianza, siendo estas:
Ejemplo 21. El INTT indica que el 60% de los conductores usan el cinturón de seguridad. Se seleccionó una muestra al azar de 10 conductores en una autopista. ¿Cuál es la probabilidad de que 7 conductores o menos usen el cinturón de seguridad?
El experimento cumple con las características de las distribuciones binomiales.
Se define:
- X: N° de conductores que usan el cinturón de seguridad de una muestra de 10
- n = 10; Probabilidad de éxito = 60%
- P(x) = b(x; 10, 60%)
Existe una probabilidad del 83,27% de que 7 o menos conductores escogidos al azar, de una muestra de 10 conductores, usen el cinturón de seguridad.
Distribución Hipergeométrica
Cuando el experimento a realizar posee las siguientes características:- El resultado en cada prueba de un experimento se clasifica en una de dos categorías excluyentes (éxito o fracaso).
- La variable aleatoria mide el número de éxitos.
- Se realiza un número fijo de pruebas.
- Las pruebas no son independientes.
Para señalar que los valores de P(X) serán extraídos de una distribución Hipergeométrica, denotaremos: P(X) = h(x; n, N, S)
Los valores de probabilidad para cada valor de la variable aleatoria se pueden calcular a través de la siguiente fórmula:
Donde:
- C: Combinación.
- n: Número de pruebas o tamaño de muestra.
- N: Tamaño Población
- x: Es la variable aleatoria, definida como el número de éxitos.
- S: Número de Éxitos en la población.
Ejemplo 22. De los 50 trabajadores de una empresa, 40 están sindicalizados. Se toman 5 empleados al azar para formar un comité, ¿Cuál es la probabilidad de que 4 de ellos pertenezcan al sindicato?
Evidentemente un trabajador puede ser seleccionado solo una vez, lo que quiere decir que la selección se realiza sin reemplazo. Haciendo que las probabilidades de los que quedan cambie cada vez.
Se define:
- X: N° de trabajadores seleccionados que están sindicalizados, de una muestra de 5.
- N = 50;
- S = 40;
- n = 5
- P(x) = h(x; 5, 50, 40)
Se pide:
Existe una probabilidad del 43,1% que, al seleccionar una muestra de 5 trabajadores, 4 de ellos estén sindicalizados.
Construya la distribución de probabilidad
Distribución Multinomial
Cuando el experimento es aplicado a una variable cualitativa que puede tomar más de dos valores posibles.Características:
- Al llevar a cabo un experimento con esta distribución se esperan más de dos tipos de resultados.
- Las probabilidades asociadas a cada uno de los resultados son constantes.
- Cada uno de los ensayos o repeticiones del experimento son independientes.
- Número de repeticiones del experimento, n es constante.
En lo anterior debe cumplirse que:
x1 + x2 +⋯+ xk = n
Donde:
- n: Número de pruebas.
- xi: Distintos valores de la variable aleatoria que se quieren verificar.
- pi: Valor de probabilidad de un éxito de cada variable xi
Ejemplo 23. Se lanza al aire un dado normal, 5 veces, determine la probabilidad de que aparezca dos números uno, dos números tres y un número cinco.
Se define:
- n = N° de lanzamientos del dado.
- x1 = N° de veces que aparece el número 1
- x2 = N° de veces que aparece el número 3
- x3 = N° de veces que aparece el número 5
- p1 = probabilidad de que aparezca el número 1
- p2 = probabilidad de que aparezca el número 3
- p3 = probabilidad de que aparezca el número 5
n = 5
x1 = 2 p1 = 1/6
x2 = 2 p2 = 1/6
x3 = 1 p3 = 1/6
Se pide:
Existe una probabilidad menor a un 1% de que, al lanzar 5 veces un dado, se obtenga 2 números uno, 2 números tres y un cinco.
Ejemplo 24. Las probabilidades de que un delegado llegue a una cierta convención, por aire, en autobús, en automóvil o en tren, son de 0.40, 0.20, 0.30 y 0.10, respectivamente, determine cuál es la probabilidad de que entre 9 delegados seleccionados al azar en esta convención, ocurra:
a) que 3 hayan llegado por aire, 3 en autobús, 1 en auto y 2 en tren
Se define:
- n = N° de delegados escogido al azar.
- x1 = N° de delegados que llegan por aire.
- x2 = N° de delegados que llegan en autobús.
- x3 = N° de delegados que llegan en auto.
- x4 = N° de delegados que llegan en tren
- p1 – p4= probabilidades de que un delegado llegue a través de un medio de transporte respectivamente.
De lo anterior se tiene:
n = 9
x1 = 3 p1 = 40%
x2 = 3 p2 = 20%
x3 = 1 p3 = 30%
x4 = 2 p4 = 10%
Se pide:
Existe una probabilidad del 0,77% de que, de una muestra de 9 delegados, 3 hayan llegado por aire, 3 en autobús, 1 en auto y 2 en tren.
b) que 4 hayan llegado por aire, 1 en autobús, 2 en auto.
Nótese que aun cuando no se suministra información acerca del número de personas que hayan llegado en tren, se asume por defecto, como el resto que queda de los 9 una vez asignados los tres primeros medios de transporte.
Se pide:
c) que 5 hayan llegado en auto.
Se define:
- n = N° de delegados escogido al azar.
- x1 = N° de delegados que llegan en auto de un total de 9 delegados.
Así planteado, este problema se ajusta al caso binomial, por tanto P(x) = b(x; 9, 30%)
Existe una probabilidad del 7,35% de que, de muestra de 9 delegados, 5 hayan llegado en auto (y el resto en cualquier otro medio de transporte).
Distribución de Poisson
El hecho no ocurre como el resultado de un número definido de pruebas de un experimento, sino en puntos de tiempo, espacio o volumen al azar. Describe el número de veces que ocurre un evento durante un intervalo específico (el intervalo puede ser de tiempo, distancia, área o volumen).
Se le llama distribución de los "eventos raros" pues se usa como aproximación a la binomial cuando el tamaño de muestra es grande y la proporción de éxitos es pequeña.
Características:
- La variable aleatoria, es el número de veces que ocurre un evento durante un intervalo definido.
- La probabilidad de un evento es proporcional al tamaño del intervalo.
- La probabilidad de observar exactamente un éxito en el intervalo es constante.
- Los intervalos no se superponen y son independientes, es decir, la probabilidad de observar un éxito en cualquier intervalo es estadísticamente independiente de la de cualquier otro intervalo.
Esta distribución se aplica en situaciones como:
- El número de pacientes que llegan al servicio de emergencia de un hospital en un intervalo de tiempo.
- El número de radiaciones radiactivas que se recibe en un lapso de tiempo,
- El número de partos triples por año
Para denotar que los valores de probabilidad provienen de una Distribución de Poisson, se escribe: P(X) = p(x; λ)
La expresión matemática para calcular las probabilidades a través de Poisson es:
Donde:
- e: La constante 2,7182.
- λ: Número de ocurrencias por intervalo. Esperanza del número de éxitos.
- x: Valor de variable que se quiere verificar.
Ejemplo 25. Si en promedio, llegan tres pacientes por minuto al servicio de emergencia del hospital del Niño durante la hora del almuerzo. ¿Cuál es la probabilidad de que, en un minuto dado, lleguen exactamente dos pacientes? Y ¿Cuál es la probabilidad de que lleguen más de dos pacientes en un minuto dado?
Se define:
- x: Número de pacientes que llegan por minuto al hospital del niño.
- P(x) = p(x;3)
De lo anterior se tiene:
- λ= 3 (pacientes/minuto)
Se pide:
- P(x=2) = ¿?
- P(x>2) = ¿?
Existe una probabilidad del 22,4% de que lleguen dos pacientes en un minuto cualquiera a la sala de emergencia del hospital de niños.
Existe una probabilidad de un 57,68% de que, en un minuto cualquiera lleguen más de dos pacientes a la emergencia del hospital de niños.
Ejemplo 26. Un fabricante de tejidos de lana afirma que el promedio de defectos en sus productos es uno por cada dos yardas cuadradas. ¿Cuál es la probabilidad de que una yarda cuadrada de su producto muestre tres defectos?
En este caso se define:
- x: Número de defectos que presenta por yarda cuadrada.
Se sabe:
- λ= 1 (defecto/2 yardas cuadradas)
- P(x) = p(x; 1)
- P(x=3 defecto/yarda cuadrada) = ¿?
Si 1 (defecto/2 yardas cuadradas) entonces 0,5 defecto/ yarda cuadrada
Ahora:
- λ= 0,5 (defecto/ yarda cuadrada)
- P(x) = p(x; 0,5)
Existe una probabilidad de un 6,13% de que en una yarda cuadrada escogida al azar se encuentren 3 defectos



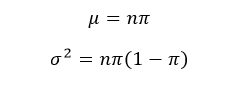












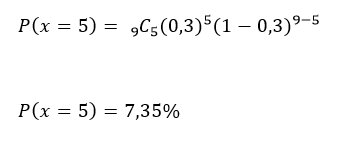

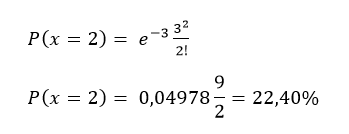
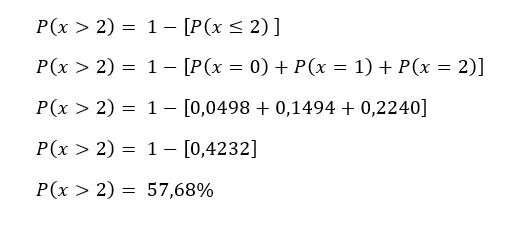

No hay comentarios.:
Publicar un comentario