Probabilidad
Valor entre cero (0) y uno (1), inclusive, que describe la posibilidad (probabilidad, viabilidad) relativa de que ocurra un evento. Estos valores se pueden expresar como un número decimal (0,10), como una fracción (1/10) o como porcentaje (10%)Definiciones Básicas.
Experimento Aleatorio: Proceso que lleva a la ocurrencia de una y sólo una de varias observaciones posibles, no pudiéndose predecir de antemano cuál de ellos va a producirse en una experiencia concreta. Por ejemplo, el lanzamiento de una moneda. Se puede observar cómo se lanza, pero no se sabe si caerá “cara” o “sello”.Experimento Determinista: Proceso que lleva a la ocurrencia de una y sólo una de varias observaciones posibles, que, realizado en las mismas condiciones, se obtiene siempre el mismo resultado (de éstos se ocupa la Física).
Resultado: La consecuencia de un experimento en particular. Los resultados posibles del experimento “lanzar una moneda” son dos: “que caiga cara” o “que caiga sello”.
Evento: Conjunto de uno o más resultados de un experimento. Subconjunto de un espacio muestral. Por ejemplo, del experimento “lanzar dos monedas al aire”, un evento podría ser: “que se obtengas dos caras”
Los eventos pueden ser:
- Seguros: cuando se tiene certeza que ocurrirán. Tienen un valor de probabilidad asignado de uno (1). Ejemplo “Obtener una cara o un sello al lazan una moneda”.
- Imposible: cuando se tiene certeza que no ocurrirán. Tiene un valor de probabilidad asignado de cero (0). Ejemplo “Obtener un ocho (8) al lanzar un dado”.
- Independientes: Cuando la probabilidad de ocurrencia de uno NO afecta la probabilidad de ocurrencia del otro.
- Dependientes: Cuando la probabilidad de ocurrencia de uno SI afecta la probabilidad de ocurrencia del otro.
- Mutuamente Excluyente: La ocurrencia de un evento significa que ninguno de los otros puede ocurrir al mismo tiempo. Un ejemplo lo es el experimento “sexo de una persona”, cuyos resultados posibles son: “M” y “F”. El evento “Hombre” es excluyente del Evento “Mujer”. Una misma persona no puede cumplir con ambos eventos a la vez.
- Colectivamente Exhaustivo: Por lo menos uno de los eventos debe ocurrir al realizar el experimento.
- Complementario: Cuando uno es la negación de otro y en conjunto hacen el espacio muestral.
Espacio muestral
Conjunto de todos los resultados posibles producto de la realización de un experimento en particular.Ejemplo 1. determine el espacio muestral y defina algunos eventos en los siguientes experimentos: a) lanzamiento de un dado, b) lanzamiento de dos dados, c) lanzamiento de dos monedas.
Enfoque para asignar probabilidades
Existen varios enfoques que dictaminan la forma de asignar probabilidades. La teoría de la probabilidad estudia los distintos enfoques a fin de poder asignar valores de probabilidad a distintos eventos. En el diagrama siguiente se muestra dichos enfoques.Probabilidad Clásica
Se basa en la suposición de que los resultados de un experimento son igualmente viables:
Ejemplo 2. Considere un experimento de tirar un dado. ¿Cuál es la probabilidad de que el evento “salga un número par” ocurra?
Los resultados posibles son:
- Salga uno (1)
- Salga dos (2)
- Salga tres (3)
- Salga cuatro (4)
- Salga cinco (5)
- Salga seis (6)
En el conjunto de resultados posibles (espacio muestral) que son igualmente probables hay tres resultados favorables (dos, cuatro, seis), por tanto:
Probabilidad Empírica
Basada en las frecuencias relativas. La probabilidad de que un evento suceda se determina:
Ejemplo 3. El 1 de febrero de 2003, explotó el trasbordador espacial Columbia. Este fue el segundo desastre en 113 misiones espaciales para la NASA. Con base a esta información, ¿Cuál es la probabilidad de que una misión futura se realice con éxito?
Lo anterior se puede tomar como un estimado de la probabilidad. Con base a la experiencia pasada, la probabilidad de que una misión del trasbordador espacial en el futuro sea exitosa es de 98%.
Probabilidad Subjetiva
Posibilidad (probabilidad) de que un evento en particular suceda, que asigna un individuo con base en la información disponible. Algunos ejemplos de probabilidad subjetiva son:
- Estimar la probabilidad de que la selección de fútbol venezolana clasifique para el próximo mundial.
- Estimar la probabilidad que apruebe el presente curso de estadística.
Reglas para Calcular Probabilidades
Hasta ahora ya definimos las distintas estrategias que se siguen a la hora de asignar probabilidades, ahora nos centraremos en el cálculo de probabilidad para dos a mas eventos.Regla de Adición
La regla de adición aplica cuando se quiere conocer la probabilidad que ocurra la unión de los eventos (el evento A ó el evento B), se denota como P(A o B). Es importante distinguir cuando se trata de eventos mutuamente excluyentes y cuando no.
En términos generales, P(A o B) = P(A) + P(B) – P(A y B)
Cuando los eventos a estudiar son mutuamente excluyentes, entonces se tiene que (A y B) = Ø, quedando la regla de adición como: P(A o B) = P(A) + P(B)
Ejemplo 4. ¿Cuál es la probabilidad de que una carta elegida de una baraja estándar sea un Rey o un Corazón?
No se trata de eventos excluyentes ni exhaustivos. Se tiene que:
Por lo tanto:
P(A o B) = P(A) + P(B) – P(A y B)
P(A o B) = 4/52 + 13/52 – 1/52
P(A o B) = 30,77%
Ejemplo 5. En un proceso de llenado automático de empaques de azúcar, se revisa 4000 paquetes.
¿Cuál es la probabilidad de que un paquete le sobre o le falte peso?
Por ser eventos excluyentes se tiene que:
P(A o C) = P(A) + P(B)
P(A o C) = 0,025 + 0,075
P(A o C) = 0,10
Si los eventos son exhaustivos (como es el caso) se cumple la regla del complemento:
P(A) = 1 – P(~A)
P(A o C) = P(~B) = 1 – P(B) = 1 – 0,90 = 0,10
Regla de la Multiplicación
Se emplea cuando se quiere conocer la probabilidad de que dos eventos sucedan de manera simultánea. Aquí es importante distinguir cuando se tratan de eventos independientes o dependientes.
Si los eventos SON independientes, aplica la regla especial, la cual reza:
P(A y B) = P(A)P(B)
Si los eventos NO SON independientes, aplica la regla general, la cual reza:
P(A y B) = P(A)P(B|A)
Probabilidad Condicionada
En ocasiones la probabilidad de ocurrencia de un evento está sujeta (depende) de la ocurrencia o no de algún otro suceso (evento). Generalmente de la dependencia de un evento con respecto a otro está determinado por la forma en que se lleve a cabo el experimento.Ejemplo 6. Una encuesta realizada a un grupo de ejecutivos de GM, Co. Reveló que el 60% de ellos hizo alguna reservación en una línea aérea el año pasado. Se seleccionan dos miembros de forma aleatoria. ¿Cuál es la probabilidad de que ambos hayan hecho una reservación en una línea aérea el año pasado?
Se definen los eventos:
E1: Que el primer Ejecutivo seleccionado haya hecho reservación.
E2: Que el segundo Ejecutivo seleccionado haya hecho reservación.
P(E1) = 0,6
P(E2) = 0,6
Son eventos independientes, por tanto
P(E1 y E2) = P(E1)P(E2)
P(E1 y E2) = (0,6)(0,6) = 0,36
Ejemplo 7. En una caja hay 10 CD vírgenes, de los cuales se sabe 3 están defectuosos. Si se extraen secuencialmente dos CD de manera aleatoria, sin reposición. ¿Cuál es la probabilidad de que ambos sean defectuosos?
Se definen los eventos:
D1: Primer CD seleccionado es defectuoso.
D2: Segundo CD seleccionado es defectuoso.
Se tienen que:
P(D1) = 3/10
P(D2) = 3/9 si en primer CD no es defectuoso. Lo cual se denota por: P(D2|~D1)
P(D2) = 2/9 si el primer CD seleccionado era defectuoso. Se denota por: P(D2|D1)
P(D1 y D2) = P(D1)P(D2|D1)
P(D1 y D2) = (3/10)(2/9) = 6/90
Ejemplo 8. Determine las probabilidades conjuntas de todos los casos posibles…
Tablas de Contingencia
También conocidas como tablas de doble entrada, se pueden presentar tanto en términos absolutos como relativos, para las segundas, hay tres variaciones: relativas respecto al total, relativas respecto a las columnas y relativas respecto a las filas.Probabilidad Total
Sea A1, A2,..., An un sistema completo de sucesos tales que la probabilidad de cada uno de ellos es distinta de cero, y sea B un suceso cualquier del que se conocen las probabilidades condicionales P(B|Ai), entonces la probabilidad del suceso B viene dada por la expresión:Ejemplo 9. Una compañía dedicada al transporte público explota tres líneas de una ciudad, de forma que el 60% de los autobuses cubre el servicio de la primero línea, el 30% cubre la segunda y el 10% cubre el servicio de la tercera línea. Se sabe que la probabilidad de que, diariamente, un autobús se averíe es del 2%, 4% y 1%, respectivamente, para cada línea. Determina la probabilidad de que, en un día, un autobús sufra una avería.
Se definen los eventos:
A1: “Unidades de Trasporte de la línea 1”
A2: “Unidades de Trasporte de la línea 2”
A3: “Unidades de Trasporte de la línea 3”
B: “Sufrir una avería”
Se conoce que:
P(A1) = 60% P(A2) = 30% P(A3) = 10%
P(B|A1) = 2% P(B|A2) = 4% P(B|A3) = 1%
Determine:
P(B) = ¿?
P(B) = P(A1). P(B|A1) + P(A2). P(B|A2) + P(A3). P(B|A3)
P(B) = (0,6) (0,02) + (0,3) (0,04) + (0,1) (0,01)
P(B) = 0,012 + 0,012 + 0,001
P(B) = 0,025
Teorema de Bayes
El teorema de Bayes permite calcular la probabilidad del evento A condicionada a la ocurrencia del evento B, a partir de la probabilidad de que ocurra el evento B condicionada a la ocurrencia del evento A. permite calcular la probabilidad de ocurrencia de las causas, a partir de las consecuencias que han podido ser observadas.Derivación de la fórmula:
Ejemplo 10. En un país existe una enfermedad peculiar, la cual la padecen el 5% de la población. Existe una técnica de diagnóstico, pero no es muy precisa. Evidencias históricas demuestran que, si una persona tiene la enfermedad, la probabilidad de que la prueba indique su presencia es de 90%. Y existe una probabilidad del 15% de que la prueba indique su presencia aun cuando en realidad no tiene la enfermedad.
Supongamos que se selecciona al azar a un habitante de ese país, le realizamos la prueba y ésta indica que la enfermedad está presente. ¿Qué probabilidad hay de que la persona realmente padezca la enfermedad?
Se definen los eventos:
A1: “Tiene la enfermedad”
A2: “No tiene la enfermedad”
B: “La prueba indica que la enfermedad está presente”
De lo anterior se tiene:
P(A1) = 5%;
P(A2) = 1- P(A) = 95% (son eventos complementarios)
P(B|A1)) = 90%
P(B|A2) = 15%
P(A1|B) = ¿?
Con la ayuda del teorema de Bayes podemos determinar la probabilidad a posteriori:
Ejemplo 11. Un fabricante de equipos electrónicos usa un microchips en su producto. Este lo obtiene de tres proveedores. A continuación, se muestra la cantidad de microchips que se compran a cada empresa y sus tasas de fallos:
Si todos se encuentran en un mismo lote, si se escoge uno al azar y está defectuoso, ¿Cuál es la probabilidad que sea de SS?
Se definen los eventos:
A1: “El chips pertenece a HE”
A2: “El chips pertenece a SS”
A3: “El chips pertenece a CC”
B1: “El chips está defectuoso”
B2: “El chips no está defectuoso”
Se conocen las siguientes probabilidades:
Principios de Conteo
Fórmula de la Multiplicación
Se utiliza para calcular el número de arreglos posibles para dos a más grupos. Si hay m formas de hacer una cosa y n formas de hacer otra, hay m.n formas de hacer ambas. Esta regla se puede extender a más de dos eventos.
Ejemplo 12. Si usted tiene 8 camisas distintas y 6 pantalones. ¿Cuántos arreglos puede formar?
En este caso hay (m)(n) = (8)(6) = 48 arreglos posibles.
Fórmula de la Permutación
Si interesa conocer el número posibles de arreglos cuando solo hay un grupo de objetos y el orden en que se dispongan es importante, se emplea la fórmula de la permutación:
Ejemplo 13. En una competencia donde participan 5 atletas, se premiaran solo los tres primeros lugares, con oro, plata y bronce, según terminen. ¿De cuántas formas diferentes puede culminar la competencia?
Y si se ofreciesen premiaciones a los cinco competidores ¿Cuántos arreglos distintos se formarían?
Fórmula de la Combinación
Si interesa conocer el número posibles de arreglos cuando solo hay un grupo de objetos y el orden en que se dispongan NO es importante, se emplea la fórmula de la combinación:
Ejemplo 14. En una competencia donde participan 5 atletas, se seleccionarán solo los tres primeros lugares, para que pasen a la siguiente etapa. ¿De cuántas formas diferentes puede culminar la competencia?

















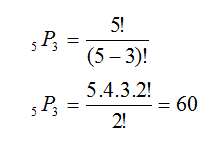


Para ser asertivo en los negocios y en la vida en general, debemos contar con herramientas (conocimientos) que nos permitan hacer posible tomar decisiones sobre la base de la certeza, es decir, tomar decisiones en función al "Yo sé" y no en el "Yo creo". Una de estas poderosas herramientas es el estudio de las Probabilidades...Definitivamente esta herramienta capacita a quien las emplea de un conocimiento adecuado a la hora de tomar decisiones.
ResponderBorrarExcelente observación sr Nadal. Las herramientas estadísticas le permitirán apoyar la toma de decisiones. Ahora podrá seleccionar entre alternativas, de forma más objetiva y menos “vísceral”. Pero adicionalmente, entender conceptos básicos estadísticos lo convertirá en un “Mejor consumidor de Información”. Será más fácil distinguir entre, “lo que le dicen” y lo que “le quieren decir”. Incluso, empezará a cuestionar la forma en la que la “información” que le estén suministrando se determinó.
BorrarEste comentario ha sido eliminado por el autor.
ResponderBorrarApreciados compañeros quiero comentarles que la probabilidad nace con el deseo del hombre de conocer con certeza los eventos del futuro, a través de la historia se han desarrollado varios enfoques conceptuales diferentes para definir la probabilidad y determinar los valores probables de los cuales voy a mencionarles tres que son:
Borrar1.- El Enfoque Clásico.
2.- El Enfoque de Frecuencia Relativa.
3.-El Enfoque Subjetivo.
Aclarando un poco mas La Probabilidad mide la frecuencia con la que se obtiene un resultado al llevar a cabo un experimento aleatorio, del que se conocen todos los resultados posibles, bajo condiciones suficientemente estables, La teoría de la probabilidad se usa extensamente en áreas como la estadísticas, la física, la matemática, la ciencia y la filosofía, para sacar conclusiones sobre la probabilidad de sucesos potenciales, la teoría de la probabilidad es la parte de las matemáticas que estudia los fenómenos aleatorios, los cuales deben contraponerse a los fenómenos a los cuales se esperan resultados únicos y previsibles siempre que se realice bajo la mismas condiciones de esta forma poseen un conjunto de de alternativas. Actualmente la teoría de la probabilidad encuentra aplicación en las mas variadas ramas del conocimiento que incluye también el área de las finanzas.
En el mismo orden de ideas, la teoría de de la probabilidad es una de las bases fundamentales de la estadística, gracias a ella se establece la posibilidad relativa de que ocurra un determinado evento, el cual puede expresarse matemáticamente, basado en experimentos aleatorios, determinación de resultados, y los tipos de eventos, utilizando para ello el espacio muestral y la determinación del enfoque para asignar probabilidades (clásica, empírica o subjetiva). Estos elementos se unen con las reglas para el cálculo de las probabilidades (Adición y multiplicación), el cual nos permite aplicaciones y resultados, para un sinfín de casos y situaciones a nivel empresarial. En la actualidad (año 2.017) en el campo de la administración de empresas, la estadística probabilística es una herramienta fundamental para la toma de decisiones económicas y financieras, para lograr maximizar las ganancias y reducir las pérdidas a la mínima expresión posible en las organizaciones, de allí la importancia del manejo y conocimiento de sus principios y sus conceptos. Manuel S.Valera S. Administración de Empresas.
BorrarExcelente síntesis de lo que es “Teoría de la probabilidad” sr Valera. Para resumir, el cálculo de probabilidad permite transformar la “incertidumbre” en “riesgo”.
BorrarAl hablar de probabilidad nos referimos al estudio de la ocurrencia de eventos aleatorios, con la finalidad de presentar un esquema que nos ayude analizar los riesgos del día a día, y a su vez mis permita facilitar la toma de decisiones, considerando también todas las variables que puedan afectar el producto final. Maria ortega/administración de empresa
ResponderBorrarExacto Sra. Ortega. Básicamente comprender estadística nos permitirá procesar más información y de manera más eficiente. Nos convertirá en “mejores consumidores de información"
BorrarLas herramientas que se utilicen en el área financiera nos facilitan la toma de decisiones, una de ellas es la teoría de la probabilidad que nos permiten predecir el comportamientos de ciertas situaciones que ocurren dentro de la organización. Las probabilidades son de gran utilidad al momento de invertir en un proyecto, lo cual nos permite predecir el comportamiento de las posibles ganancias o perdidas sea el caso y si la empresa esta en la capacidad de querer invertir o no y la manera de hacerlo. Es importante recordar que dentro de las probabilidades siempre van a existir los riesgos que dependerán de cada situación y necesidades. Al detectar los riesgos nos permitirá asesorarnos de la manera correcta para minimizar los mismos. Yris Garrido
ResponderBorrarAun cuando la experiencia es importante, hay que dejar de un lado las decisiones viscerales y ponderar todas las alternativas. En ese sentido, la estadística es nuestra mejor aliada.
BorrarEste comentario ha sido eliminado por el autor.
ResponderBorrarLa herramienta permite registrar los datos en tablas y su representación en gráficos. Permite también, calcular los parámetros estadísticos, que describen el conjunto estudiado, así, se pueden tomar decisiones con mayor comprensión de la información en forma ordenada.
ResponderBorrarEste comentario ha sido eliminado por el autor.
ResponderBorrarBeatriz Yejas
ResponderBorrarEl metodo de probabilidad nos permite obtener la frecuencia de los acontecimientos mediante la realizacion de un analisis aleatorio del cual se conocen todos los resultados posibles bajo las condiciones suficientemente estables, se centra en el porcentaje de posibilidades de que algo ocurra. Debido a esto es empleada en muchas ocasiones para tomar decisiones o hacer apuestas ya que esta cuenta con su propia lógica matemática, siempre expresada en porcentajes, es la caracteristica de un evento que hace que existan razones para creer que algo se puede realizar.
Es una herramienta de gran importancia ya que nos permite predecir sucesos a futuros, es la parte de las matemáticas que estudia los fenómenos aleatorio,en materia presupuestaria para la formulación del presupuesto de una organización es de gran ayuda para evaluar el comportamiento de cada partida y obtener parámetros estadísticos que sirven como referencia para la elaboración del presupuesto de una empresa y una distribución equitativa que permita garantizar el uso eficiente de los recursos enmarcada en la consecución del logro de las metas.
ResponderBorrarLa teoría de la probabilidad se sustenta en el estudio de las frecuencias de ocurrencias de determinados eventos en un contexto dado, de modo que la utilización de esta como herramienta de la estadística, ayudaría a diseñar un modelo adecuado y ajustable a la representación y definición de las situaciones fortuitas que pudiesen acontecer en una empresa, sirviendo en gran medida, como elemento evaluador tanto de oportunidades y riesgos que se pudieran tener al momento de una toma de decisiones, que mediante la aplicación de la teoría de la probabilidad, sería un proceso más asertivo en medio de la incertidumbre, como variable al entorno donde se desenvuelve la empresa.
ResponderBorrarLa teoría de la probabilidad tiene como fin examinar las formas y medios para obtener esas medidas de certeza, así como encontrar los métodos de combinarlos cuando intervienen varios sucesos en un experimento o prueba.
ResponderBorrarla probabilidad es el fundamento necesario de la estadística, además de otras disciplinas como la matemática, física entre otras.
El objetivo del calculo de probabilidades es el estudio de métodos de análisis del comportamiento de fenómenos aleatorios
La Probabilidad en la Estadistica es una herramienta que ha permitido a profesionales de todo ramo, conocer los posibles resultados de un experimento o un proyecto a futuro, estudiando las posibilidades de exito o fracaso, observando todos los escenarios posibles bajo condiciones estables o normales.
ResponderBorrarTeniendo información como esta, podemos conocer la viabilidad o rentabilidad de cualquier proyecto o estudio que como individuos u organizaciones se planteen, esperando siempre resultados positivos y conocer los riesgos que se tomaran al momento de convertir ese experimento en algo concreto.
Se reunirá entonces la cantidad de datos ya sean cualitativos o cuantitativos, de individuos, grupos o series de hechos, analizar, comprimir y resumir información recogida y para ello ese resultado debe ser de fácil entendimiento para cada usuario que haga uso de la misma para la toma de decisiones.
Dicho esto podemos entonces decir que la Probabilidad es una gran herramienta para carreras como la Administración y/o Contaduría.
La Estadística: Es una ciencia que utilizamos en la cotidianidad y es de suma importancia ya que con ella podemos estudiar la información de los consumidores, en la ámbito contable brinda un gran aporte cuando se realizan auditorias, el principal objetivo de la estadística son las referencia acerca de una población con base en la información contenida en muestra. En la teoría de probabilidad, a la hora de realizar estudio nos permiten analizar diversas probabilidades o posibilidades de un evento utilizando herramientas, donde al tener mayor precisión de los análisis y procesar la variedad en los datos brinden certeza a la investigación. Maria Bracho /contaduría
ResponderBorrarMuchas veces se habla de la estadística aplicada al mercado, de la estadística financiera, etc., pero en realidad la estadística está aplicada en la mayoría de los ámbitos de la vida cotidiana de cada individuo; ya que las estadísticas se basan en estudiar la información recopilada u obtenida mediante diversas herramientas (encuestas, observación, entrevistas) y organizarlas de manera que sea funcional y efectiva tanto para una empresa/organización como para la vida personal de un individuo en particular. Al saber interpretar los datos, enseguida gozamos de una ventaja y podemos adelantarnos a posibles resultados y así obtener lo que sea más conveniente (dado sea el caso). Es muy importante saber recopilar los datos, ya que un dato errado puede afectar de manera negativa la interpretación de éste y a su vez la toma de una decisión puede ser totalmente equivocada puesto que la fuente lo está. Al final, las estadísticas nos arrojan suficiente información para no dejar todo librado al azar, queda en cada individuo interpretar y aplicar la información de manera eficaz, eficiente y conveniente.
ResponderBorrarFreddy J. Torrealba C. V.- 14.915.726.
Muchas veces se habla de la estadística aplicada al mercado, de la estadística financiera, etc., pero en realidad la estadística está aplicada en la mayoría de los ámbitos de la vida cotidiana de cada individuo; ya que las estadísticas se basan en estudiar la información recopilada u obtenida mediante diversas herramientas (encuestas, observación, entrevistas) y organizarlas de manera que sea funcional y efectiva tanto para una empresa/organización como para la vida personal de un individuo en particular. Al saber interpretar los datos, enseguida gozamos de una ventaja y podemos adelantarnos a posibles resultados y así obtener lo que sea más conveniente (dado sea el caso). Es muy importante saber recopilar los datos, ya que un dato errado puede afectar de manera negativa la interpretación de éste y a su vez la toma de una decisión puede ser totalmente equivocada puesto que la fuente lo está. Al final, las estadísticas nos arrojan suficiente información para no dejar todo librado al azar, queda en cada individuo interpretar y aplicar la información de manera eficaz, eficiente y conveniente.
ResponderBorrarFreddy J. Torrealba C. V.- 14.915.726.
Las probabilidades son muy útiles, ya que pueden servir para desarrollar estrategias. Por ejemplo, algunos automovilistas parecen mostrar una mayor tendencia a aumentar la velocidad si creen que existe un riesgo pequeño de ser multados; los inversionistas estarán más interesados en invertirse dinero si las posibilidades de ganar son buenas. El punto central en todos estos casos es la capacidad de cuantificar cuan probable es determinado evento. En concreto decimos que las probabilidades se utilizan para expresar cuan probable es un determinado evento.
ResponderBorrarCon el paso del tiempo el hombre siempre busca la forma o la manera de descubrir lo desconocido, por consiguiente llegamos a esta teoria LA TEORIA DE LA PROBABILIDAD, que juega un papel muy importante en la vida del hombre, puesto que es cien por ciento util en todos los campos de estudio y aprendizaje en que se necesite condiciones de azar.
ResponderBorrarDebemos tomar los puntos clave, tener el espacio muestarl o un resultado ya esperado en una determinada posicion y poder obtener dar un valora ese ejemplo por lo cual se debe analizar cada paso a realizar para obtener un resultado mas especifico y saber algunas ecuaciones que nos ayuden a dar respuestas a ellos de una manera mas rapida y sencilla.